決定係數
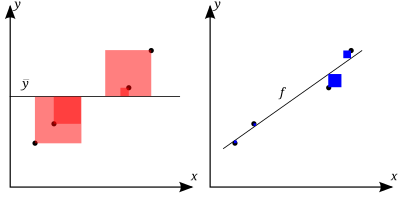
決定係數,或稱判定係數(英語:Coefficient of determination,記為R 2),在統計學中用於度量應變數的變異中可由自變量解釋部分所占的比例,以此來判斷迴歸模型的解釋力。[1][2][3]
對於簡單線性回歸而言,決定係數為樣本相關係數的平方。[4]當加入其他回歸自變量後,決定係數相應地變為多重相關係數的平方。
假設一數據集包括y1,...,yn共n個觀察值,相對應的模型預測值分別為f1,...,fn。定義殘差ei = yi − fi,平均觀察值為
於是可以得到總平方和
殘差平方和
由此,決定係數可定義為
參考文獻[編輯]
- ^ Steel, R. G. D.; Torrie, J. H. Principles and Procedures of Statistics with Special Reference to the Biological Sciences. McGraw Hill. 1960.
- ^ Glantz, Stanton A.; Slinker, B. K. Primer of Applied Regression and Analysis of Variance. McGraw-Hill. 1990. ISBN 0-07-023407-8.
- ^ Draper, N. R.; Smith, H. Applied Regression Analysis. Wiley-Interscience. 1998. ISBN 0-471-17082-8.
- ^ Devore, Jay L. Probability and Statistics for Engineering and the Sciences 8th. Boston, MA: Cengage Learning. 2011: 508–510. ISBN 0-538-73352-7.
|





