非線性降維

高維數據，意味着數據需要多於兩個或三個維度來表示，一般很難被解釋。一種簡化的方法是假設數據嵌在高維空間的一個非線性流形上。如果這個流形維數足夠低，那麼數據可以在低維空間中被可視化。

非線性降維的應用

使用非線性降維算法（Manifold Sculpting）產生的二維（縮放和旋轉）散點圖。

使用線性降維算法PCA產生的二維散點圖，數據分佈並不那麼有條理

考慮以矩陣（或數據庫）表示的數據集，其中每行都代表描述某物特定實例的一組屬性（或特徵）。如果屬性的數量很大，那麼可行行空間的增長速度是指數級的（例如有$f$個屬性，每個屬性均具有$k$種可能的選擇，則所有可能的屬性為$k^{f}$）。維度越大，對空間進行採樣就越困難。這導致了處理高維數據的算法時間複雜性非常高。許多機器學習算法在處理高維數據時很吃力，而將數據縮降維會使算法更有效率，並能幫助機器學習算法做出更準確的預測。

人類往往難以理解高維數據。因此將數據減進行降維對於可視化非常有用。

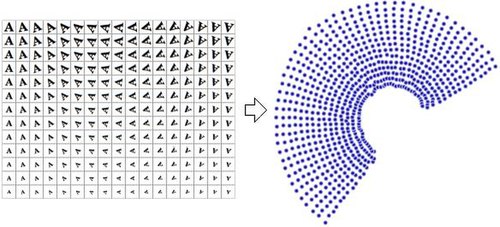
數據的降維表示通常被稱為 "內在變量"，即它們是數據產生的價值。例如，考慮一個包含字母 "A" 經過縮放和旋轉的圖像的數據集，每張圖片有32×32像素，可以表示為長度為1024的向量。每一行都是1024維的空間（漢明空間）中，二維流形上的一個樣本。由於數據僅通過縮放和旋轉得到，所以本質維度是2；而字母 "A" 的形狀或外觀則不是內在變量（因為數據集中所有元素該特徵均相同）。非線性降維將拋棄相關的信息（字母 "A"），只保留變化的信息（縮放和旋轉）。右圖展示了該數據集的部分樣本，及通過使用非線性降維算法（Manifold Sculpting）將數據降到二維的結果散點圖。

作為對比，右圖使用線性降維算法PCA（主成分分析），將同樣的數據集降為二維，可以發現結果並沒有採用非線性降維算法好。這表明從該流形上採樣得到的高維向量以一種非線性的方式變化。

非線性降維在計算機視覺領域有所應用。例如一個使用相機在封閉的靜態環境中導航的機械人，相機得到的圖像可以視為從高維空間流形採樣得到的樣本，該流形的內在變量代表機械人的位置和朝向。

下面列舉了一些非線性降維算法。

流形學習算法

自組織映射

主條目：自組織映射

自編碼器

主條目：自編碼器

自編碼器是一個前饋神經網絡，其訓練目標為恆等映射，即從一個向量映射到同一個向量。用於降維時，其部分隱藏層只包含少量神經元。此時，網絡必須學會用較少的維度編碼向量，並同時能將將其解碼。因此，網絡的前半部分（編碼器，Encoder）從高維空間映射到低維空間，後半部分（解碼器，Decoder）從低維空間映射到高維空間。

核方法的主成分分析

主條目：核主成分分析

核主成分分析（Kernel Principal Component Analysis，KPCA）是最常用的降維算法之一。PCA首先計算$m\times n$矩陣$\mathbf {X}$的協方差矩陣：

$C={\frac {1}{m}}\sum _{i=1}^{m}{\mathbf {x} _{i}\mathbf {x} _{i}^{\mathsf {T}}}.$

然後將數據投影到協方差矩陣的前k個特徵向量上。而KPCA首先將數據變換到更高維的空間，然後計算變換後數據的的協方差矩陣：

$C={\frac {1}{m}}\sum _{i=1}^{m}{\Phi (\mathbf {x} _{i})\Phi (\mathbf {x} _{i})^{\mathsf {T}}}.$

然後和PCA一樣，將數據投影到協方差矩陣的前k個特徵向量上。該方法使用了核方法來避免大量的運算，整個過程可以在沒有實際計算$\Phi (\mathbf {x} )$的情況下執行（當然，$\Phi$必須被選擇）。不幸的是，為特定問題選擇一個合適的核函數並不容易，在使用普通核函數時，KPCA的表現不一定好；例如在瑞士卷流形（Swiss roll manifold）上的表現不佳。有部分方法通過構造依賴於數據的核矩陣達成較好的表現（例如 Laplacian Eigenmaps），該類方法可以看作KPCA的特殊情況。

KPCA有一個內部模型，因此它可以用來將不在訓練集中的點映射到嵌入。

等距特徵映射

主條目：等距特徵映射

拉普拉斯特徵映射

主條目：拉普拉斯矩陣

參見

• Discriminant analysis
• Elastic map
• Feature learning
• Growing self-organizing map (GSOM)
• Pairwise distance methods
• Self-organizing map (SOM)

外部連結

• Isomap
• Generative Topographic Mapping
• Mike Tipping's Thesis （頁面存檔備份，存於互聯網檔案館）
• Gaussian Process Latent Variable Model
• Locally Linear Embedding （頁面存檔備份，存於互聯網檔案館）
• Relational Perspective Map （頁面存檔備份，存於互聯網檔案館）
• Waffles （頁面存檔備份，存於互聯網檔案館） is an open source C++ library containing implementations of LLE, Manifold Sculpting, and some other manifold learning algorithms.
• Efficient Dimensionality Reduction Toolkit homepage
• DD-HDS homepage
• RankVisu homepage
• Short review of Diffusion Maps
• Nonlinear PCA by autoencoder neural networks （頁面存檔備份，存於互聯網檔案館）