圖論術語
| 此條目可參照英語維基百科相應條目來擴充。 |
圖論中有許多專有名詞,此處總結了一些名詞的一般意義和用法。
基本術語[編輯]
一個圖(一般記作)由兩類元素構成,分別稱為「頂點」(或節點、結點)和「邊」。每條邊有兩個頂點作為其端點,我們稱這條邊「連接」了它的兩個端點。因此,邊可定義為由兩個頂點構成的集合(在有向圖中為有序對,見下文「方向」一節)。
圖也可以用其他模型來表示,如定義在頂點集合上的二元布爾函數,或者方形(0,1)-矩陣。
頂點或邊上有標號的圖稱為有標號的,否則為無標號的。它們的區別在於,無標號的圖並沒有為頂點或邊指定一個特定的順序。
圖的標號一般指按某一規則為圖的頂點或邊指定一個標號。標號通常是自然數,且一般互不相同。

一個超邊是允許連接任意多個(可以多於兩個)頂點的「邊」。含有超邊的「圖」稱為超圖。邊可視為恰連接兩個頂點的超邊,因此圖可視為一種特殊的超圖。
空圖或禿圖是沒有邊的圖。
如果一個圖有無窮多的頂點和/或邊,則稱其為無窮的,否則為有窮的。如果一個圖是無窮的,但每個頂點的度(見下)是有限的,則稱為局部有窮的。一般假定「圖」指有窮圖。
兩個圖和,如果存在與之間的一一對應,使得圖中兩個頂點相連當且僅當它們在圖中的對應頂點相連,則稱圖和 同構,記作。類似地,如果僅僅是到的映射而不一定是一一對應,則稱此映射是到的同態。
彼得森圖[編輯]
圖論中最有名圖之一。
邊[編輯]
一條邊一般表示為連接其兩個端點的曲線。以兩個頂點、為端點的邊一般記作、或。一條邊連接兩個頂點u、v時,稱u與v相鄰。圖的邊集一般記作,當不發生混淆時可簡記為。
補圖[編輯]
圖的補圖是這樣一的圖,它的點集與相同,而每條邊存在於中當且僅當它不存在於中。
頂點[編輯]
一個頂點一般表示為一個點或小圓圈。一個圖的頂點集(點集)一般記作,當不發生混淆時可簡記為。圖的階為其頂點數目,亦即||。
度[編輯]
若兩個點之間有一條邊,則這兩個點相鄰。關聯一個點的邊的條數稱為是度數(degree)或價(valency)。特別的,若不是多重圖時,它等於這一點的鄰點個數。
一個頂點被稱作孤立頂點,當它的度數為。
的最小度記為
的最大度記為
的平均度記為
稱為k-正則的,當的所有頂點都有相同的頂點度k。特別的,3-正則圖被稱作立方圖。
獨立集[編輯]
一個圖的獨立集是圖中一些兩兩不相鄰的頂點所形成的集合。
二分圖[編輯]
圖G是二分圖當且僅當它的點集V能被劃分成兩塊X和Y,使得對於G中的任意一條邊,它有一個端點屬於X而另一個端點屬於Y。
哈密爾頓圖[編輯]
環[編輯]
看環(圖論)。
結[編輯]
距離[編輯]
距離是兩個頂點之間經過最短路徑的邊的數目,通常用表示。
頂點的偏心率(eccentricity),用來表示連接圖中的頂點到圖中其它頂點之間的最大距離,用符號表示。
圖的直徑(diameter),表示取遍圖的所有頂點,得到的偏心率的最大值,記作。相對於直徑的一個概念是圖的半徑(radius),表示圖的所有點的偏心率的最小值,記作。這兩者間的關係是:
柯尼斯堡七橋問題[編輯]
圖論中著名的問題。
立方圖[編輯]
連通圖/連通性[編輯]
稱是連通的,如果非空圖的任意兩個頂點之間均有一條路相連。
稱是k-連通的,如果非空圖的任意兩個頂點之間都有條獨立路相連。k-連通的的另外一個定義是:若,且對任意滿足的子集均有是連通的,則稱是k-連通的。由門格爾定理,易知這兩個定義是等價的。通過k-連通的概念,定義使得是k-連通的最大整數稱作的連通度。
類似的,還可以引入k-邊連通的概念:稱一個的圖是k-邊連通的,如果對任意一個滿足的邊的集合,均是連通的。同樣,的邊連通度是使得是k-邊連通的最大整數。
旅行推銷員問題[編輯]
計算機科學中最有名的問題之一。
歐拉路徑[編輯]
匹配[編輯]
平面圖[編輯]
庫拉托夫斯基定理描述了有點平面圖。有名的歐拉公式也說:V-E+F=2. 這是歐拉示性數。
嵌入[編輯]
強連通分量[編輯]
橋[編輯]
路徑[編輯]
路徑(walk),又譯作途徑。一個長度為的路徑是一個非空的頂點和邊的交錯序列,使得對於所有均有。特別的,當時,稱這個路徑是閉的(closed);當路徑中的頂點互不相同,得到的一條路。[1]
樹[編輯]

連通無圈圖稱為樹,一般記為T。其中,度數為1的頂點稱為葉子,否則稱為內點。有時我們會從樹中選出一個頂點作為特殊頂點,稱之為根以示區分,此時稱此樹為有根樹。有根樹常作為有向無環圖來處理。
樹T的連通子圖稱為T的子樹。
樹也是一個團的森林。
森林[編輯]
無環(不一定連通)圖稱為森林,森林F的子圖稱為F的子森林。
如果圖G的一個生成子圖是樹,則稱該子圖為生成樹。
星是僅有一個頂點不是葉子的樹。星也可以表示為完全二分圖K1,n。
縮圖[編輯]
隨機圖[編輯]
團[編輯]
圖中的團是由圖中兩兩相鄰的頂點構成的集合。
Utility graph[編輯]
完全圖[編輯]
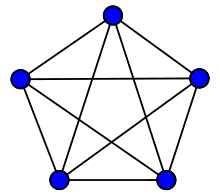
完全圖是所有頂點兩兩相鄰的圖。n階完全圖,記作Kn。如圖所示為K5。n階完全圖有n(n-1)/2條邊。
網絡流[編輯]
重要的計算機科學、最優化理論、與算法學的題目。也看最大流最小割定理。
圍長[編輯]
圍長定義為圖所包含的最短環長,也被稱為"girth"。
線圖[編輯]
相鄰[編輯]
兩頂點相鄰,意思是之間有一條邊。
葉子[編輯]
看以上的樹術語。
正則圖[編輯]
自環[編輯]
一個自環是兩個端點為同一頂點的邊。如果有多於一條邊連接同一對頂點,則它們均被稱為重邊。一個圖的重數是重複次數最多的邊的重複次數。如果一個圖不含自環或重邊,則稱為簡單圖。多數情況下,如無特殊說明,可以假定「圖」總是指簡單圖。
着色[編輯]
圖着色問題包含四色定理,數學中最有名的問題之一。現代的證明用電腦、文章很長。
子圖[編輯]
兩個圖G和H,如果V(H)是V(G)的子集且E(H)是E(G)的子集(當然,E(H)中只能包含將V(H)中的頂點相連的邊)則稱H是G的子圖。如果圖G和H不相等,即V(H)是V(G)的真子集或E(H)是E(G)的真子集,則稱H是G的真子圖。如果H是G的子圖或者存在一個G的子圖與H同構,則稱G包含H。
如果圖G的子圖H滿足V(H)=V(G),即圖H包含圖G的所有頂點,則稱H是G的支撐子圖或生成子圖。
如果圖G的子圖H滿足邊(u,v)在圖H中當且僅當邊(u,v)在圖G中,即圖H包含了圖G中所有兩個端點都在V(H)中的邊,則稱H是G的導出子圖。
對於圖的某個性質而言,如果圖G具有此性質而G的任一真子圖都不具有此性質,則稱G是具有該性質的極小圖。類似地,如果圖G具有此性質而任一以G為真子圖的圖都不具有此性質,則稱G是具有該性質的極大圖。
最短路問題[編輯]
重要的計算機科學、與算法學的題目。也看Dijkstra算法、Kruskal算法、等。
定理術語[編輯]
- 彼得森定理
- 布魯克斯定理
- 柯尼格引理
- 柯尼格定理 (圖論)
- 庫拉托夫斯基定理
- 拉姆齊定理(而且看拉姆齊理論)
- 門格爾定理(Menger's Theorem)
- 圖特定理
- Vizing定理
- 最大流最小割定理
圖的方向[編輯]
有向無環圖[編輯]
代數圖論[編輯]
不變量[編輯]
虧格(幾何、拓撲)[編輯]
看以上的平面圖。
譜圖論[編輯]
參考來源[編輯]
- ^ R.Diestel. 图论 第四版. 高等教育出版社. : 10.
參見[編輯]
- 圖
- 圖論
- 圖論話題列表
- 數學
- 離散數學
- 組合數學
- 算法
- 計算機科學
- 最優化
- 人工智能(神經網格)
- 連接組(承現峻,connectome)
- 網格科學
- 費曼圖(Feynman diagram、物理、量子力學、統計力學)
| ||||||||||||||||||||||||||||||||||||||||||||||




































