解迷宫算法

本页使用了标题或全文手工转换
维基百科，自由的百科全书
正在走木制迷宫的机器人

解迷宫算法又称走迷宫算法是一种自动求解迷宫的方法。解迷宫算法主要可以分成两大类，一种是用来走没走过的迷宫且无法得知整个迷宫的方法，这类方法较常见的有随机老鼠算法、沿墙法、普莱吉算法和特雷莫算法；另一类是适用于可以一次看到整个迷宫时所使用的方法，这类方法较常见的有死路填充法和最短路径算法。

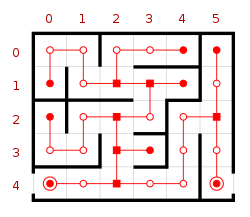
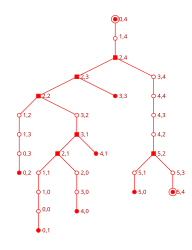
不包含循环路径的迷宫称为“简单连接”或“完美”的迷宫，其等价于图论中的树。解迷宫算法与图论密切相关。直观上来说，若以适当的方式拉开迷宫中的路径，其结果可能会是一棵树。[1][2]

概述[编辑]

一个典型的解迷宫算法会

  • 取描述某个迷宫环境的消息做为输入。例如：用一个矩阵，矩阵中每个数字用来代表迷宫里面的一格；
  • 并且经过一些运算之后，给出有关“应该如何移动”的指示作为输出。例如：+1, +1 表示“x坐标和y坐标都要各加1”。

算法的输入根据其类型而定：有的算法是假设了“能以鸟瞰式的方式看到整个迷宫”为前提，所以输入时会描述整个迷宫的环境；有的算法是设计给机器人实际在迷宫里走迷宫的，所以输入时仅会描述机器人视线范围内的环境[3]。 解迷宫算法在人工智慧、机器人学甚至是游戏编程（游戏内NPC的寻路算法）等领域中都有相当的应用[4][5]。

另一方面，解迷宫算法也引起了数学家的注意，因为这算法与图论中的算法有相当的关连。例如：单连通的迷宫，迷宫中的路线简单地连接着，并且不包含任何循环。这种迷宫相当于图论中的树状图：如果将迷宫中的路线拉开的话会得到类似图论中讨论的树状结构。[2]

  • 一个迷宫与其可能的路径
    一个迷宫与其可能的路径
  • 将迷宫中的路径拉开成一个树状结构
    将迷宫中的路径拉开成一个树状结构

随机老鼠算法[编辑]

这是一种非常简单的算法，可以由非常不智慧的机器人或一只普通的老鼠来实现。这个算法的内容就是单纯的延着迷宫中的路径前进，遇到岔路时，随机选择一个方向来前进。虽然这个方法最终总是能解开迷宫，但过程可能十分缓慢。[6]

沿墙法[编辑]

使用右手规则走迷宫

解迷宫算法中最著名的方法是沿墙法[7]，也称为左手规则（左手法则、左手定则）或右手规则（右手法则、右手定则）[8]。如果迷宫是单连通的，也就是说迷宫的所有墙壁都与迷宫的外边界相连，那么只要靠着迷宫的一侧墙不断前进（或者说每次遇到岔路都转向同个方向，如每次遇岔路都右转或都左转），那么就能保证不迷路地到达迷宫的出口（如果有出口的话），如果迷宫没有出口则会回到原地，且至少遍历了与该墙连接的部分旁边的每个走廊。这个算法是一个深度优先的中序树遍历。

关于为何沿墙法能解迷宫的另一个观点是基于拓朴学的解释。如果迷宫是单连通的，代表迷宫的墙壁是相连的，且没有回路[9][10]，所以在一个这样的迷宫里，每当走迷宫那个人遇到岔路，每条岔路只有可能再分岔或者是死路。这就表示如果将这迷宫化成树状图，这个树状图不会有任何互相相交的分支，且在拓朴学上它们可能可以拓朴形变为一个环[11]，然后沿墙法可简化为在这个环上从头到尾绕一圈。为了进一步推进这个想法，可留意将迷宫墙壁的连通分量组合在一起，而这些分量的边界正是迷宫的解。

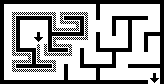
起点位于被环状通道包围之结构的中心的迷宫使用右手规则结果绕回入口

如果迷宫不是单连通的，（例如起点和终点位于被环状通道包围之结构的中心、或者路径互相交叉且能解迷宫的路径的部分被环状通道包围）则沿墙法不一定有效。

另一个须留意的点是如果不是在迷宫入口处就开始就依循沿墙法走迷宫时。如果迷宫不是单连通的，并且是在迷宫中的任意点才开始依循沿墙法走迷宫，那么可能会发现自己被困在单独一堵墙之中，该墙壁围绕着自己，并且无法返回入口也无法抵达出口，还会永远沿着这一系列的墙打转。如果是走迷宫半路上才开始依循沿墙法走迷宫时，应尝试记住或标记迷宫中的一个点，并从那个点开始依循沿墙法走迷宫，因为沿墙法总是会带你回到同一个地方，如果第二次又绕回同一个点，那么就能断定迷宫不是单连通的，这时就应该切换到另一面尚未依循的墙或方向。有关的替代方法可以参考下面列出的普莱吉算法。

普莱吉算法[编辑]

左图：依循左手规则走迷宫陷入循环；
右图：依循普莱吉算法成功走出迷宫

不相交（存在不与外边界相连的墙之迷宫、或边界不封闭的迷宫）的迷宫可以使用沿墙法解决。然而，如果从迷宫内部某点才开始求解迷宫，那么使用沿墙法可能会沿着一道不与出口相连的墙，并且不断绕着这些墙打转。普莱吉算法（Pledge algorithm；名称取自约翰·普莱吉（John Pledge））可以解决这一问题。[12][13][14]

普莱吉算法是为了要能够避开障碍物而设计的，需要走迷宫那个人也许随便选择一个方向来做前进方向。当依循这个算法走迷宫那个人撞到一块障碍物的时候，他会转方向，同时会一只手会触摸着旧东西一边转，并且会数旋转的角度（例如顺时针当正，逆时针当负）， 并且不断尝试把总共转了的角变为0度（例如：如果走迷宫者左转了，并走了一格就撞到可以右转的地方的话，他会马上右转）。当走迷宫那个人转到面向回他原本的前进方向时，总共转的角（图里的“S”）会是0度，而走迷宫那个人会离开旧障碍物，继续向着他原本的方向走。[12]

只有当“总共转的角”（图里的“S”）和“当前方向”（图里的“H”）都为零时，手才会从墙上移开。这个算法能够帮走迷宫的那个人克服像拉丁字母“G”那样形状的无限循环陷阱（使用沿墙法时会在“G”形迷宫墙壁上不断打转）。

一个仅仅留意著自己目前方向的算法会陷入一个死循环：以“G”形迷宫为例，一个仅仅留意著自己目前方向（图里的“H”）的算法会让走迷宫那个人走到最右下角向内凸出来那堵墙时左转，并且走回去左手边那一块那里，然后开始无限打转。普莱吉算法不会犯这个错，因为在最右下角向内凸出来那堵墙的那一点“总共转的角”不是0度（360度不当0度）， 所以那个人会沿着墙边走到去左下角那一个出口。[12]

该算法允许拥有指南针的人从任何有限二维迷宫的内部任何点找到前往外部出口的路，而不管从迷宫中的何处才开始依循此算法，也就是无论从迷宫中的何处作为初始位置都能找到出口。然而，这个算法在做相反的事情时不起作用，即找到从迷宫外面的入口到迷宫内某个目的地的路。

特雷莫算法[编辑]

依循特雷莫算法解一个迷宫。大绿点表示当前位置，小蓝点表示路径上有1个记号，红色叉叉表示路径上有2个记号。一旦找到出口，就会标出通过单一记号的路径

特雷莫算法是由法国数学家查尔斯·皮埃尔·特雷莫（英语：Charles Pierre Trémaux）发明的[15]一种能有效地找到迷宫出路的方法[16][17]。这个方法需要在地板上画线来标记路径，只要迷宫有清楚定义了的通道就保证有效[18]。这种做法会把每条通道分成“没去过的”、“去过一次的”、和“去过两次的”三种。并且会接着以下的规则运行：

  • 每次第一次行经一条路时要做记号，这个记号要是在这条路的两端都看得到的。所以如果那个记号是物理性（而不是用电脑记住）的话，这个记号要在这条路的两端都留下；
  • 不进入做记号的位置上有两个记号的路径里；
  • 接着有三个可能性：
    • 如果走到去一个什么记号都没有的岔路那里，那么就是选择一条路走，并且做好记号；
      • 如果走进来那条路只有一个记号的话，那就回头，“转身返回”，再多做一次记号。这个情况表示前面是死路；
      • 如果都不是的话，则任意选择具有最少记号的剩余路径走，并且做好记号。

“转身返回”规则有效地将任何带有循环的迷宫转换为单连通的迷宫；每当我们找到一条可以循环的路径时，我们就将其视为死路并返回。如果没有这条规则，也就是说若遇到迷宫回路时没有回头，而是随意地走另一条路，就有可能切断能进入迷宫中尚未探索部分的通道。

在用这个算法走到去出口后，只要跟着“仅有做一次记号”的路径当指示就能返回起点。如果迷宫根本没有出口的话，这个方法会带着走迷宫的人回去起点，而且每条路都会有两个记号。在后者这个情况下，每条路恰好走过两次，而两个方向各一次。这个走路过程被人称之为双向双重跟踪（bidirectional double-tracing）[19]。

从本质上讲，这种在19世纪发现的算法在大约在发现后的一百年后被用作深度优先搜索。[16][17]

死路填充算法[编辑]

外部视频链接
video icon 迷宮策略：死路填充法. [2022-09-06]. （原始内容存档于2020-07-27）. 
video icon 解迷宮演算法. [2022-09-06]. （原始内容存档于2021-02-06）. 
做完死路填充算法的迷宫

死路填充算法（dead-end filling）是一个解迷宫算法，做法如下：[20]把迷宫里的死路全部找出来；再用记号填满所有死路，每条死路填到第一个岔路那里；这样就可以很容易看到整个迷宫里有哪些路是能走的。这种做法可以拿来说明一个完全已知的迷宫，例如是在纸上面玩的迷宫游戏，但是因为这个算法要求解迷宫那个人能够从迷宫上方鸟瞰看到整个迷宫，所以无法用于未知的迷宫。

死路填充算法不会意外地切掉从起点到终点的路线，因为算法的每一个步骤都保留了迷宫的拓朴结构。此外该过程不会提早结束，因为最终的结果不会包含任何死路。因此，如果所解的迷宫是一个完美的迷宫（没有循环回路的迷宫），那么做完死路填充算法后将会留下迷宫的解，也就是从入口到出口的路线；如果所解的迷宫带有一些循环回路，那么做完死路填充算法后将会保留迷宫的所有可行解，仅此而已。[21]

递归法[编辑]

假如解迷宫的那个人知道整个迷宫的路线（例如是纸上面玩的迷宫游戏），那么透过一个简单的递归算法就能将这个迷宫从起点走到终点。这个算法会接收一个起始的座标值：X和Y。如果X和Y的值不在一堵墙上面的话，这个算法会在所有周围邻近的X和Y值调用自己，确保调用的是之前没有使用过的这些X和Y值，而如果他找到终点的X和Y值，那他会以走过那些路以X和Y值的型式记下来一条正确路线。以下是这种算法用Java编程语言写出来的样本： 

int[][] maze = new int[width][height]; //儲存整個迷宮的陣列，每個X和Y值都代表迷宮中的一個位置，「1」代表路，「2」代表牆。
boolean[][] wasHere = new boolean[width][height];
boolean[][] correctPath = new boolean[width][height]; // 迷宮解法陣列，等一下用來記下來解迷宮的正確路線。
int startX, startY; //設兩個變數做起點的X和Y值。
int endX, endY; //設兩個變數做終點的X和Y值。

public void solveMaze() {
   maze = generateMaze(); //產生出整個迷宮，「 1 」代表路，「 2 」代表牆。
   for (int row = 0; row < maze.length; row++)  
      // 將 boolean Arrays 設定為預設值
      for (int col = 0; col < maze[row].length; col++){
         wasHere[row][col] = false;
         correctPath[row][col] = false;
      }
   boolean b = recursiveSolve(startX, startY);

// 會得出一個 Boolean 的陣列（correctPath）
// 其中「真」（true）值會用來代表解迷宮的正確路線。
// 如果b為「假」（false），那就代表個迷宮根本是無解的。
}

public boolean recursiveSolve(int x, int y) {
   if (x == endX && y == endY) return true; // 如果到了終點，回傳「真」值出去。
   if (maze[x][y] == 2 || wasHere[x][y]) return false;  
// 如果撞到牆或已經來過這一點，回傳「假」值出去。
   wasHere[x][y] = true;
   if (x != 0) // 檢查一下是不是到了最左的邊界。
      if (recursiveSolve(x-1, y)) {
         correctPath[x][y] = true;
         return true;
      }
   if (x != width - 1) // 檢查一下是不是到了最右的邊界。
      if (recursiveSolve(x+1, y)) {
         correctPath[x][y] = true;
         return true;
      }
   if (y != 0)  // 檢查一下是不是到了最底的邊界。
      if (recursiveSolve(x, y-1)) {
         correctPath[x][y] = true;
         return true;
      }
   if (y != height - 1) // 檢查一下是不是到了最頂的邊界。
      if (recursiveSolve(x, y+1)) {
         correctPath[x][y] = true;
         return true;
      }
   return false;
}

铲起迷宫算法[编辑]

铲起迷宫算法（maze-routing algorithm）是一种用来找出一个迷宫里任意两点之间之路线的方法。[22]这个算法能够得知两点之间是不是真有路通到，而且无论个迷宫多大都好，他都能让一个从迷宫内部开始走、记忆力有限、事前完全不知道个迷宫是什么样子的个体成功地解完迷宫，只是要求走迷宫的个体记住4个变量就可以找到这条路线出来。但是这个算法不保证能找到最短路径。

铲起迷宫算法用了曼哈顿距离（Manhattan distance；简称“MD”）的概念。这个概念指的是两点之间的空间可以用格子代表，而假设一个个体只有沿着格子的边线行走的话，在两点之间穿梭都会有很多条“最短路线”，这些路线的长度就是以所谓的MD计算的。以下是一段伪代码： 

Point src, dst;// 起點和終點的座標
// 「cur」表示現在的位置。
int MD_best = MD(src, dst);//儲存走迷宮個體和目的地之間的最短MD。
// 一條好（productive）的路線就是一條能夠讓MD最小化的路線。
while(cur != dst){
    if(there exists a productive path){
        Take the productive path;
    }else{
        MD_best = MD(cur, dst);
        Imagine a line between cur and dst; // 想像一條目前位置和目的地之間的線。
        Take the first path in the left/right of the line;
        while(MD(cur, dst) != MD_best || there does not exist a productive path) {
            Follow the right-hand/left-hand rule; // 使用沿牆法（左右手法則）。
    }
}

最短路径算法[编辑]

更多信息：寻路
一个有多种解且没有死路的迷宫，在其中找到最短路径可能很有用
使用广度优先搜索来解迷宫

当迷宫有多个解时，就会希望能找到入口到出口的最短路径。有几种算法能找到最短路径，其中大部分来自图论。一种方法是使用广度优先搜索来找寻解迷宫的最短路径，而另一种方法——A*搜索算法则是使用了启发式的技术。广度优先搜索使用队列以距离递增的顺序走访迷宫的单元格，每个被走访的单元格都需要追踪它与起点的距离、哪个相邻的单元格更靠近起点导致它被加进队列中。找到迷宫的终点后，沿着单元格往回找到起点则为最短路径。最简单形式的广度优先搜索有其局限性，例如在加权图中找到最短路径。

参见[编辑]

参考文献[编辑]

  1. ^ YouTube上的Maze to Tree
  2. ^ 2.0 2.1 Sadik, Adil MJ and Dhali, Maruf A and Farid, Hasib MAB and Rashid, Tafhim U and Syeed, A. A comprehensive and comparative study of maze-solving techniques by implementing graph theory. 2010 International Conference on Artificial Intelligence and Computational Intelligence (IEEE). 2010, 1: 52–56. 
  3. ^ Provost, Jefferson; Benjamin Kuipers; Risto Miikkulainen. Self-organizing distinctive-state abstraction for learning robot navigation. Connection Science. 2006, (18.2). doi:10.1080/09540090600768609. 
  4. ^ Mishra, Swati; Bande, Pankaj. Maze solving algorithms for micro mouse. 2008 IEEE International Conference on Signal Image Technology and Internet Based Systems (IEEE). 2008: 86–93. 
  5. ^ Wyard-Scott, L; Meng, Q-HM. A potential maze solving algorithm for a micromouse robot. IEEE Pacific Rim Conference on Communications, Computers, and Signal Processing. Proceedings (IEEE). 1995: 614–618. 
  6. ^ Babula, Michał. Simulated maze solving algorithms through unknown mazes. Organizing and Program Committee (Citeseer). 2009, 13. 
  7. ^ Saman, Abu Bakar Sayuti and Abdramane, Issa, Solving a reconfigurable maze using hybrid wall follower algorithm (PDF), 2013 
  8. ^ Zarkasi, Ahmad and Ubaya, Huda and Amanda, Cora Deri and Firsandaya, Reza. Implementation of ram based neural networks on maze mapping algorithms for wall follower robot. Journal of Physics: Conference Series (IOP Publishing). 2019, 1196 (1). 
  9. ^ Fritzke, Bernd. A growing neural gas network learns topologies. Advances in neural information processing systems. 1994, 7. 
  10. ^ Maze Types and Topology: A Summary. Amazeing Art. （原始内容存档于2018-09-14）. 
  11. ^ YouTube上的Maze Transformed
  12. ^ 12.0 12.1 12.2 Klein, Rolf and Kamphans, Tom. Pledge's Algorithm-How to Escape from a Dark Maze. Algorithms Unplugged (Springer). 2011: 69–75. 
  13. ^ Abelson; diSessa, Turtle Geometry: the computer as a medium for exploring mathematics, 1980, ISBN 9780262510370 
  14. ^ Seymour Papert, Uses of Technology to Enhance Education (PDF), MIT Artificial Intelligence Memo No. 298, June 1973, （原始内容 (PDF)存档于2017-07-06） 
  15. ^ Public conference, December 2, 2010 – by professor Jean Pelletier-Thibert in Academie de Macon (Burgundy – France) – (Abstract published in the Annals academic, March 2011 – ISSN 0980-6032)
    Charles Tremaux (° 1859 – † 1882) Ecole Polytechnique of Paris (X:1876), French engineer of the telegraph
  16. ^ 16.0 16.1 Even, Shimon. Graph Algorithms (2nd ed.). Cambridge University Press. 2011: 46–48. ISBN 978-0-521-73653-4. 
  17. ^ 17.0 17.1 Sedgewick, Robert. Algorithms in C++: Graph Algorithms (3rd ed.). Pearson Education. 2002. ISBN 978-0-201-36118-6. 
  18. ^ Lucas, Édouard. Récréations mathématiques Volume I. Récréations mathématiques. Gauthier-Villars. 1882. 
  19. ^ Maze Activity Using Maze Solving Algorithms (PDF). cs4all.org. （原始内容 (PDF)存档于2020-03-28）. .
  20. ^ Maze Classification. astrolog.org. [2022-09-06]. （原始内容存档于2019-04-06）. 
  21. ^ Fattah, Mohammad and Airola, Antti and Ausavarungnirun, Rachata and Mirzaei, Nima and Liljeberg, Pasi and Plosila, Juha and Mohammadi, Siamak and Pahikkala, Tapio and Mutlu, Onur and Tenhunen, Hannu. A low-overhead, fully-distributed, guaranteed-delivery routing algorithm for faulty network-on-chips. Proceedings of the 9th International Symposium on Networks-on-Chip. 2015: 1–8. 

外部链接[编辑]

取自“https://zh.100ke.info/w/index.php?title=解迷宮演算法&oldid=80499048”